Fonctions : Généralités

I. Définition

Soit $mathcal{D}$ , un ensemble de nombres réels.
Définir une fonction $f$ sur l'ensemble $mathcal{D}_{f}$ , c'est associer à chaque réel $x$ de $mathcal{D}_{f}$ un unique réel $y$ .
On note :
$begin{array}{lccc} f : & mathcal{D}_{f} & rightarrow & mathbb{R} & x & mapsto & y=f(x) end{array}$

$mathcal{D}_{f}$ est l'ensemble de définition de la fonction $f$

$x$ est un antécédent de $y$ par la fonction $f$

$y = f(x)$ est l'image de $x$ par la fonction $f$

Remarque : $x$ est une variable qu'on peut remplacer par une autre lettre : $t mapsto f(t)$
Attention : $f(x)$ est un nombre, alors que $f$ est une fonction (une boîte noire).

Exemples :

On note la température d'une ville entre 8h et 20h. A chaque instant $t$ compris entre [8 ; 20], on associe la température mesurée f(t).
Ainsi s'il fait 10°C à 9h, on note : $f(9) = 10$ .
L'ensemble de définition de $f$ est [8 ; 20].

Soit g la fonction définie sur [-4 ; 7] par : $g(x) = 3x^2 + 2x -1$
L'ensemble de définition de g est [-4 ; 7].
On associe le nombre -2 à 3 × (-2)² + 2 × (-2) - 1 = 7.
Ceci se note : g(-2) = 7.

Soit h la fonction définie par : $x mapsto dfrac{1}{x-3}$ .
$h(6) = dfrac{1}{3}$ .
L'image de 3 par h n'existe pas.
L'ensemble de définition de h est $mathbb{R}backslashlbrace3rbrace$ .

II. Représentation graphique

Définition :

Dans un plan muni d'un repère, la courbe représentative de la fonction $f$ est l'ensemble des points $text{M} (x~;~y)$ tel que :

L'abscisse $x$ appartient à l'ensemble de définition de $f$ ;

L'ordonnée $y$ est l'image de $x$ par $f$ : $y = f(x)$ .

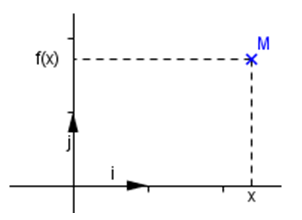Fonctions Généralités - seconde : image 1

Exemple : soit $f$ la fonction définie sur $mathbb{R}$ par $f(x) = (x - 2)^2 - 5$ .
Table de valeurs :

$x$	-1	0	1	1,5	1,75	2	2,25	2,5	3	4
$f(x) = (x - 2)^2 - 5$	4	-1	-4	-4,75	-4,94	-5	-4,94	-4,75	-4	-1

Résolution graphique (unité le centimètre) : 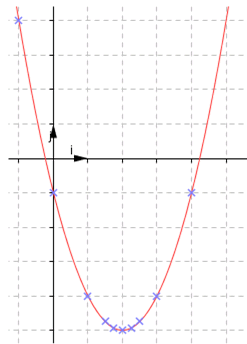Fonctions Généralités - seconde : image 2

Résoudre : $f(x) = 1,25$

Résolution graphique :
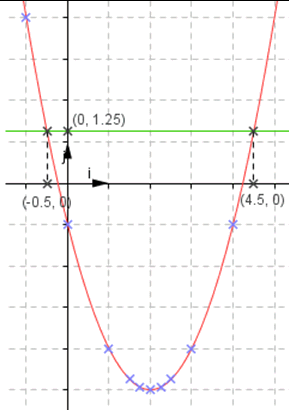Fonctions Généralités - seconde : image 3

S = {-0.5 ; 4.5}

Résolution algébrique :
Supposons qu'il existe un réel $x$ vérifiant $f(x) = dfrac{5}{4}$
D'où : $(x - 2)^2 - 5 = dfrac{5}{4}$
$Rightarrow (x - 2)^2 = dfrac{25}{4} Rightarrow (x - 2)^2 - dfrac{25}{4} = 0 Rightarrow left(x - 2 - dfrac{5}{2} right) left(x - 2 + dfrac{5}{2} right) =0 Rightarrow x = dfrac{9}{2} text{ ou } x = -dfrac{1}{2}$
Vérification : $f left(dfra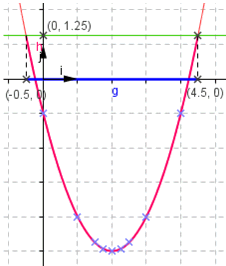c{9}{2} right) = dfrac{5}{4}$ et $f left(-dfrac{1}{2} right) = dfrac{5}{4}$ .
S = $lbrace -dfrac{1}{2} ; dfrac{9}{2} rbrace$ .

Résoudre $f(x) < 1,25$ graphiquement revient à :
Fonctions Généralités - seconde : image 4

Fonctions Généralités - seconde : image 4

D'où : S = ]-0.5 ; 4.5[

Résoudre : $f(x) = -6$

Résolution graphique :
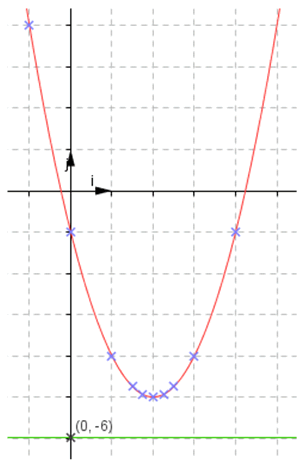Fonctions Généralités - seconde : image 5

S = $emptyset$

Résolution algébrique :
Supposons qu'il existe un réel $x$ vérifiant $f(x) = -6$
D'où : $(x - 2)^2 - 5 = -6$
$Rightarrow (x - 2)^2 = -1$ Un carré est toujours positif, ainsi il y a contradiction.
S = $emptyset$

III. Variation d'une fonction

1. Fonctions croissantes

Définition :

On dit qu'une fonction est croissante sur un intervalle I lorsque :
pour tous a et b $in$ I, on a : $a le b Rightarrow f(a) le f(b)$ .

Remarque : l'ordre est conservé.
Représentation graphique : 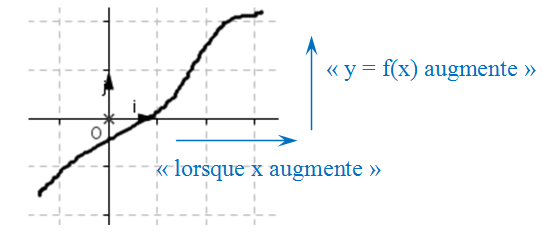Fonctions Généralités - seconde : image 6

Exemple :
La fonction $f$ définie par : $f (x) = (x - 2)^2 - 5$ est croissante sur l'intervalle [2 ; 4] (voire sur [2 ; + $infty$ [).

2. Fonctions décroissantes

Définition :

On dit qu'une fonction est décroissante sur un intervalle I lorsque :
pour tous a et b $in$ I, on a : $a le b Rightarrow f(a) ge f(b)$ .

Remarque : l'ordre est inversé.
Représentation graphique : 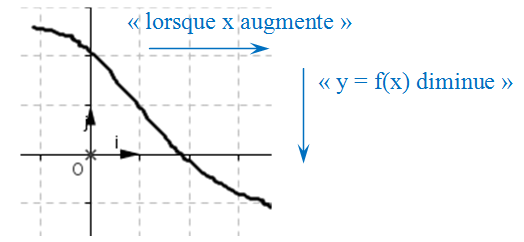Fonctions Généralités - seconde : image 7

Exemple :
La fonction $f$ définie par : $f (x) = (x - 2)^2 - 5$ est décroissante sur l'intervalle [-1 ; 2] (voire sur ]- $infty$ ; 2]).

3. Tableau de variation

Le sens de variation d'une fonction $f$ est résumé par un tableau.
Exemple : Le tableau de variation de la fonction $f$ définie par : $f (x) = (x - 2)^2 - 5$ est :
$begin{tabvar}{|c|CCCCC|} hline x & -infty & & 2 & & +infty hline f(x) & & decroit & niveau{1}{2} -5 & croit & hline end{tabvar}$

4. Extrémum

Définition :

Soit $f$ une fonction définie sur $mathcal{D}_{f}$ et un réel $a in mathcal{D}_{f}$ .
$f(a)$ est le maximum M de la fonction $f$ sur $mathcal{D}_{f}$ si pour tout $x$ de $mathcal{D}_{f}$ , on a : $f(x) le f(a)$ .
$f(a)$ est le minimum m de la fonction $f$ sur $mathcal{D}_{f}$ si pour tout $x$ de $mathcal{D}_{f}$ , on a : $f(x) ge f(a)$ .

Exemple : la fonction $f$ définie par : f $(x) = (x - 2)^2 - 5$ a pour minimum -5. Il est atteint en 2.
Sur l'intervalle [-6 ; -3], $f$ a pour maximum 59 atteint en -6.

MES COURS DE FONCTIONS

Fonctions : Généralités

I. Définition

II. Représentation graphique

III. Variation d'une fonction

1. Fonctions croissantes

2. Fonctions décroissantes

3. Tableau de variation

4. Extrémum